Low growth temperature GaAs microbolometers

This paper is abstracted from:

J. M. Lewis, D. P. Neikirk, and S. M. Wentworth, "Low growth temperature GaAs microbolometers," 15th International Conference on Infrared and Millimeter Waves, R. J. Temkin ed., Dec. 10-14, 1990, pp. 398-400.

Low growth temperature GaAs (LTGaAs) microbolometers

Jason M. Lewis*, Stuart M. Wentworth⁺, and Dean P. Neikirk

Microelectronics Research Center, Department of Electrical and Computer Engineering
The University of Texas at Austin
Austin, Texas 78712

* current address: Texas Instruments, Dallas, TX
+ current address: Electrical Engineering Department, Auburn University, Auburn, AL 39849

ABSTRACT

Microbolometers with a large negative temperature coefficient have been fabricated using an epitaxial GaAs layer grown at low temperature (LTGaAs). The detector elements used have potential in composite bolometer structures where high dR/dT materials can be used without having to be impedance matched to the antenna structure. The LTGaAs material exhibited a thermally activated conduction mechanism (E_a ~ 0.3 eV) with temperature coefficients of -0.05 K^-1 and -0.02 K^-1 at 110 K and 290 K respectively. Thermal impedance calculations suggest that the negative temperature coefficient produces filamentary electrical paths. Intrinsic dc detector responsivities as high as 10⁸ V/W have been extracted from I-V measurements.

1. BACKGROUND

Conventional microbolometers for use as far infrared detectors operate by using a planar antenna to capture electromagnetic radiation which is absorbed by a detector element attached to the antenna. A signal is caused by a change in resistance of the detector element upon heating. In conventional microbolometers, the detector element is electrically attached to the antenna and must be impedance matched to it in order to absorb radiation. Bismuth is generally used for this material because it is one of the few materials whose resistivity allows for impedance matching to antennas with impedances of 100 - 200 [Omega]. Composite microbolometers have also been demonstrated [1] in which the temperature sensing element is in close thermal contact, but is electrically isolated from the antenna load. This design allows the use of materials which can be chosen to maximize dR/dT of the detector element to achieve greater responsivities. A higher responsivity would provide a much easier means of detecting low power levels.

2. DETECTOR MATERIALS

Most metals have very similar temperature coefficients (alpha) of around 0.003, with a being defined as

(1)

In general, metals with the highest resistivity will exhibit the highest dR/dT. Tellurium (a semi-metal) is one of the few conductive elements with a resistivity higher than bismuth, and has been used in composite bolometer structures [1]. Ordinary doped semiconductors are relatively insensitive to temperature changes, and intrinsic semiconductors are difficult to fabricate in microbolometer form. One approach to finding a practical material with a higher dR/dT is to use epitaxial GaAs which is grown at much lower temperatures than normal (referred to as LTGaAs) [2], [3]. This material, originally used to prevent back-gating in MESFETs², has a very high defect density because of its low temperature growth process. It also exhibits a strong temperature dependent resistivity. Films with excellent surface morphology can be grown epitaxially on semi-insulating GaAs, which effectively provides an electrically insulating substrate.

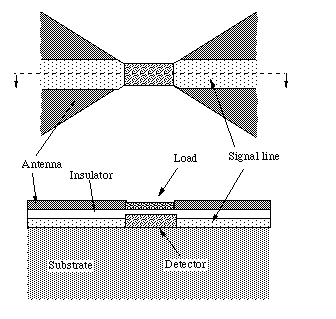
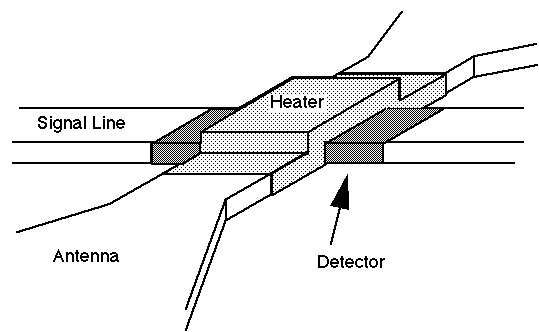
Figure 1: Bottom-view and cross-section of a composite microbolometer. The load is impedance-matched to the bow-tie antenna, and is thermally coupled to a detector.

Figure 2. Microbolometer with 10x10 um LTGaAs mesas. The gold bow-tie antenna leads are shown with a mesa used as the detector element.

3. FABRICATION

For this study, conventional microbolometers were fabricated using LTGaAs as a detector material between a bow-tie antenna structure. A 0.75 um layer of LTGaAs was grown epitaxially on a semi-insulating (SI) GaAs substrate at 270 C in an MBE system³. An antenna structure was evaporated onto the LTGaAs layer and patterned by a bi-layer photoresist liftoff process [4]. An electron beam was used to evaporate 250 Å of Cr (for adhesion) followed by a 1500 Å layer of gold for these antennas. The LTGaAs layer was then etched into 10x10 um square mesas which provided a small defined electrical connection between the two antenna leads of each microbolometer. A micrograph of the resulting structure is shown in Figure 2. Due to the pattern alignment, all LTGaAs was removed between some bow ties, allowing a measurement of parasitic leakage current through the SI GaAs substrate. For comparison, bow ties were also fabricated directly on bare SI GaAs substrates.

4. MEASUREMENTS AND DISCUSSION

Current-voltage measurements (0 to 30 volts) were made at several temperatures between 100 K to 340 K using an MMR low temperature probe station and an HP4140B. With this I-V-T data, resistance, intrinsic detector dc responsivity r*, dR/dT, and thermal impedance Z_t can be calculated. The intrinsic responsivity is given by equations 2 and 3 :

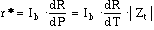(2)

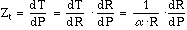(3)

where I_b is the bias current, R is the detector resistance, P is the dc power (I.V) dissipated in the detector element, and Z_t is the thermal impedance for heat escaping from the detector element. dR/dP and dR/dT can be extracted from the R-T and R-P data shown in Figure 3.

The actual bolometer temperature will rise above the ambient temperature as the power increases. An estimation of the actual detector temperature can be interpolated from Figure 3 and used to calculate (dT/dP), which is the thermal impedance Z_t. The intrinsic responsivity can also be extracted using the values of dR/dP from Figure 3. Figure 4 shows the thermal impedance and responsivity data extracted from Figure 3 for an ambient temperature of 100 K.

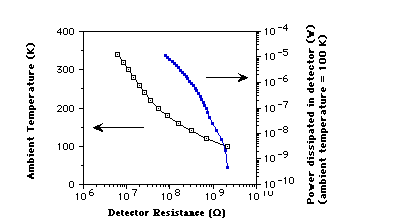
Figure 3: Detector resistance as a function of the power dissipated through the LTGaAs element or ambient temperature. All temperature data points were measured at 1 volt bias. The R-P curves cover bias voltages from 1 to 30 volts.

Figure 4: Intrinsic detector responsivity r* and thermal impedance as a function of dissipated bias power.

The R-T characteristics closely follow a thermally activated conduction mechanism with an activation energy of 0.03 eV. The temperature coefficients at 100 K and 300 K were -0.05 K^-1 and -0.02 K^-1 respectively. Measurements on bow ties without LTGaAs mesas connecting them gave resistances three orders of magnitude higher, and very small positive temperature coefficients. Bare SI GaAs substrates behaved in a very similar manner.

A rough approximation of the thermal impedance based on the LTGaAs mesa geometry and material thermal properties is given by

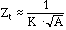(4)

where [Kappa] is the thermal conductivity and A is the contact area between the mesa and substrate [5]. This model assumes heat flow into the substrate is the dominant heat sinking process. By using the thermal conductivity of GaAs and assuming A to be the LTGaAs-GaAs interface, this value of Z_t is about 10³ K/W (compared to measured values of 10⁵ - 10⁹). This suggests that heat flow is limited by a boundary that is much smaller than the size of the LTGaAs mesa, and/or the thermal conductivity of the LTGaAs is very low. The existence of thermal filaments [6] could explain this phenomenon, in which the negative temperature coefficient provides a low resistivity path through localized regions of heating.

The effects of filamentary current paths have uncertain consequences for composite microbolometer operation. The thermal boundary caused by external heating from the composite heater element (which governs actual composite device responsivity) would be very different from the thermal filament boundaries (which govern intrinsic dc responsivity). The larger thermal boundary may reduce responsivity, but localized heating near the insulator interface may help to enhance responsivity and speed. Assuming a thermal impedance comparable to those achieved using tellurium detectors with NiCr heaters¹, a composite microbolometer responsivity of 5x10⁴ V/W might be attained using LTGaAs detectors. Further research is currently under way to evaluate the performance of such composite microbolometer structures.

4. ACKNOWLEDGEMENTS

This work was sponsored by the National Science Foundation under grant number ECS-8552868. The authors would also like to acknowledge the assistance of A. Tsao in sample preparation and etching.

5 REFERENCES

[1]. S.M. Wentworth and D.P. Neikirk, "Far-infrared composite microbolometers," IEEE MTT-S Digest 1990, pp. 1309-1310.

[2]. F.W. Smith, A.R. Calawa, C. Chen, IEEE Electron Device Lett 9, 1988, p. 77.

[3]. T.Y. Chu, A. Dodabalapur, D.P. Neikirk, and B.G. Streetman, "Properties and applications of AlGaAs grown at low temperatures," to be published in J. Crystal Growth, 1990.

[4]. D.M.Dobkin and B.D. Cantos, "Plasma formation of buffer layers for multilayer resist structures," IEEE Electron Device Lett., Vol. EDL-2, No. 9, Sept. 1981, pp. 222-224.

[5]. D.P. Neikirk, W.W. Lam, and D.B. Rutledge, "Far-Infrared microbolometer detectors," Int. J. Infrared and Millimeter Waves, Vol. 5, No. 3, 1984, pp 245-278.

[6]. E.C. Welks, R.M. Walser, R.W. Bene', and W.H. Neal, "Response of thermal filaments in VO₂ to produce laser-produced thermal perturbations," Appl. Phys. Lett. vol 26, No. 7, 1 April 1975, pp 355-357.